|
Looma
mudel maatrikskujul
Looma
mudel on maatrikskujul kirjapandav analoogselt isa
mudelile (5):
Siin
a on juhuslike aretusväärtuste n×1
vektor (n on kõigi andmestikku kuuluvate
loomade arv), ülejäänud muutujad on
defineeritud nagu isa mudeli korral.
Keskväärtused
ja dispersioonimaatriksid on:
E(a)
= 0, E(e) = 0, E(y) = Xb,
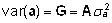 , ,
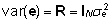 , ,
cov(a,eT)
= 0
ning
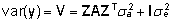
(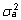 on aditiivgeneetiline dispersioon). Et
on aditiivgeneetiline dispersioon). Et 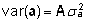 ,
siis erinevalt isa mudelist on arvestatud ka loomadevahelisi
sugulussidemeid. ,
siis erinevalt isa mudelist on arvestatud ka loomadevahelisi
sugulussidemeid.
Segamudeli
võrrand saab kuju
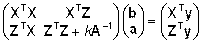 , ,
kus
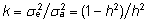 . .
NB!
Kui vektoris a esindatud loomad pole omavahel
sugulased, siis A = A-1 =
I.
Näide.
Olgu meil järgmine andmetabel:
|
Lehm
|
Ema
|
Isa
|
Uuritav
tunnus
|
|
2
|
-
|
-
|
11
|
|
4
|
-
|
-
|
7
|
|
5
|
2
|
1
|
10
|
|
6
|
2
|
1
|
8
|
|
7
|
4
|
3
|
9
|
Lehmade 2 ja 4 vanemad on teadmata. Lehmad 5 ja
6 on ET-tütred (täisõed). Lehma
2 eelistati järglaspõlvkonna tootmisel
kuna temal mõõdetud tunnuse väärtus
oli parem. Pullidel uuritavat tunnust mõõdetud
pole. Uuritava tunnuse päritavus (h2)
on 0,5. Lihtsuse mõttes on eeldatud, et ainus
mudelisse lülitatud fikseeritud efekt on üldkeskmine.
Soovime kasutada looma mudelit, valimaks välja
geneetiliselt potentsiaalilt parimaid isendeid populatsiooni
taastootmiseks.
Hindame
aretusväärtused kahel viisil: esmalt ignoreerime
loomadevahelisi sugulussidemeid ja seejärel
võtame need arvesse, ning vaatame, mil määral
nende arvestamine tulemusi muudab.
Mudel
indekskujul kirjapanduna on järgmine:
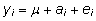 , ,
kus
µ on üldkeskmine, ai
on looma i aretusväärtus, ei
on loomale i vastav juhuslik keskkonnamõju.
Plaanimaatriksid
on
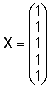 ja
ja 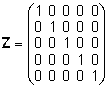
ning
vähimruutude võrrand esitub kujul
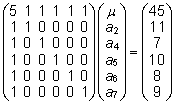 . .
Et
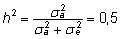 ,
siis ,
siis 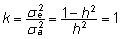 . .
(1)
Ignoreerides loomadevahelist sugulust (A
= I), on segamudeli võrrand järgmine:
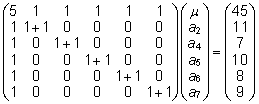
ning
selle lahendamisel saadud hinnangute vektor on
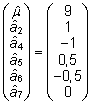 . .
Märkused.
- Kõigi
indiviidide keskmine aretusväärtus võrdub
nulliga.
- Leitud
üldkeskmise µ = 9 abil võime
iga indiviidi aretusväärtuse arvutada
valemist
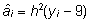 ,
kus yi on uuritava tunnuse väärtus
antud loomal. ,
kus yi on uuritava tunnuse väärtus
antud loomal.
(2)
Võtame nüüd arvesse ka loomadevahelise
suguluse, mis võimaldab arvestada selektsiooni
ja inbriidingu võimalikku mõju ning
hinnata aretusväärtused ka ilma vaatlusteta
isadele. Selleks konstrueerime aditiivse geneetilise
suguluse maatriksi A kõigi andmestikku
kuuluvate loomade (ka isade) jaoks.
 . .
Segamudeli
võrrandi (17) kirjapanekuks vajalik maatriksi
A pöördmaatriks A-1
on
 . .
Kasutades
suguluse maatriksit, hinnatakse aretusväärtused
ka isadele (a1 ja a3).
Neile efektidele vastavaid veerge eelnevalt konstrueeritud
plaanimaatriksis Z ei sisalda. Teades, et
plaanimaatriksis Z on üks rida iga vaatluse
jaoks (siin näites viis) ning üks veerg
iga geneetilise efekti jaoks (siin näites seitse,
so. viis lehma, kellel on tunnus mõõdetud
ja kaks isa), esitub Z kujul
 . .
Vähimruutude
võrrand on nüüd
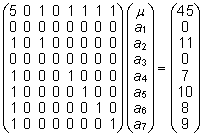 . .
Liites
vähimruutude võrrandi kordajate maatriksile
vastava alammaatriksi kA-1,
saame segamudeli võrrandi, kus on arvestatud
ka loomadevahelisi sugulussidemeid:
 . .
Selle
võrrandi lahendid on
 . .
Märkused.
- Baasloomade,
so. loomade, kelle vanemad on teadmata, aretusväärtuste
hinnangute keskmine võrdub nulliga:
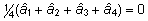 .
See on tingitud eeldusest, et baasloomad on juhuslikult
valitud baaspopulatsioonist. .
See on tingitud eeldusest, et baasloomad on juhuslikult
valitud baaspopulatsioonist.
- Järglaspõlvkonna
aretusväärtuste hinnangute keskmine on
suurem kui null:
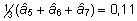 .
See väljendab nii juhusliku geenitriivi kui
ka selektsiooni mõju. Meie näites annab
kõrgema fenotüübiväärtusega
ema kaks ja madalama fenotüübiväärtusega
ema ühe järglase. Sellise valiku tulemus
peegeldub järglaste keskmises aretusväärtuses. .
See väljendab nii juhusliku geenitriivi kui
ka selektsiooni mõju. Meie näites annab
kõrgema fenotüübiväärtusega
ema kaks ja madalama fenotüübiväärtusega
ema ühe järglase. Sellise valiku tulemus
peegeldub järglaste keskmises aretusväärtuses.
- Võrdlus
isa mudeliga. Isade aretusväärtuste leidmisel
isa mudeli abil ignoreeritakse emade andmeid ning
isa 1 kaks järglast (lehmad 5 ja 6) loetakse
seeläbi poolõdedeks. Segamudeli võrrand
isade mõjude prognoosimiseks oleks:
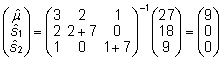 , ,
millest 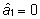 ja
ja 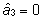 .
Seega on isa 1 ja isa 3 hinnatud geneetiliselt potentsiaalilt
võrdseteks, mis on aga looma mudelist saadud
tulemusi silmas pidades vale. .
Seega on isa 1 ja isa 3 hinnatud geneetiliselt potentsiaalilt
võrdseteks, mis on aga looma mudelist saadud
tulemusi silmas pidades vale.
|