|
Täisõvede
mudel
Juhul,
kui indiviidi aretusväärtuse hinnang baseerub
täisõvede analüüsil (analüüsitakse
mõlema vanema aditiivgeneetilist mõju
järglastele), on kasutatav mudel eelnevast pisut
erinev. Nimelt peab arvestama, et samasse täisõvede
gruppi kuuluvad loomad sarnanevad teineteisele vähemalt
kolmel põhjusel. Need on ühine isa, ühine
ema ning samad sünnieelsed ja vahel ka sünnijärgsed
kasvutingimused. Viimased võetakse geneetilises
mudelis kokku ühte, nn ühist keskkonnamõju
iseloomustavasse liidetavasse EC.
Eelnevat
arvesse võttes avaldub isa i ja ema
j järglase k fenotüübiväärtus
Pijk geneetilise mudelina
järgmiselt:
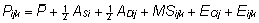 . . |
(11)
|
Siin
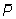 on keskmine fenotüübiväärtus
vaatlusaluses populatsioonis,
on keskmine fenotüübiväärtus
vaatlusaluses populatsioonis,
ASi ja ADij
on vastavalt i. isa aretusväärtus
ja i. isaga ristatud j. ema aretusväärtus,
ECij on i. isa ja j.
ema kõigile järglastele mõjunud
ühised keskkonna mõjud,
MSijk ja Eijk
on vastavalt Mendeli valiku mõju ja juhuslik
keskkonna mõju.
Seejuures
on Mendeli valiku mõju täisõvedele
erinev (kui see nii ei ole, on ilmselt tegu ühemuna-kaksikutega).
Statistilise
mudeli kirjapanekul arvestatakse enamasti, et
üks isaloom on paaritatud mitme emasega ning
tihti on andmete struktuur hierarhiline, st iga ema
on paaritatud vaid ühe kindla isaga. Sellisel
juhul on ema j mõju di(j)
allutatud isa i mõjule si.
Täisõvede analüüsi statistiline
mudel on järgmine:
 . . |
(12)
|
Kõrvutades
täisõvede mudeli geneetilise esituse (11)
statistilise esitusega (12) ilmneb, et andmetest ei
ole üheselt hinnatav ei Mendeli valiku mõju
ega ka püsiv keskkonnamõju -- neist esimene
ei ole statistilises mudelis eristatav mudeli jääkliikmest,
teine aga ema mõjust. Seega on statistilisest
mudelist võimalik üheselt hinnata vaid
isa mõju.
Fenotüübidispersioon
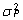 avaldub geneetilisest mudelist summana
avaldub geneetilisest mudelist summana
 . .
Sarnaselt
isa mudelile eeldatakse, et isade aretusväärtuste
dispersioon on sama suur, kui kogu populatsiooni loomade
aretusväärtuste dispersioon: 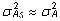 ,
sama eeldus tehakse ka emade aretusväärtuste
dispersiooni kohta: ,
sama eeldus tehakse ka emade aretusväärtuste
dispersiooni kohta: 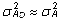 .
Seega on ka poolõvede mudeli korral pool aditiivgeneetilisest
varieeruvusest tingitud Mendeli valikust ja ei ole
statistilise mudeliga hinnatav. Et püsiv keskkonnamõju
ei ole eraldi vaadeldav ema mõjust, ei saa
eraldi hinnata ka püsivast keskkonnamõjust
tingitud varieeruvust. Seega võib fenotüübidispersiooni
komponendid grupeerida: .
Seega on ka poolõvede mudeli korral pool aditiivgeneetilisest
varieeruvusest tingitud Mendeli valikust ja ei ole
statistilise mudeliga hinnatav. Et püsiv keskkonnamõju
ei ole eraldi vaadeldav ema mõjust, ei saa
eraldi hinnata ka püsivast keskkonnamõjust
tingitud varieeruvust. Seega võib fenotüübidispersiooni
komponendid grupeerida:
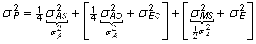 . . |
(13)
|
Statistilisest
mudelist avaldub uuritava tunnuse dispersioon summana
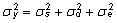 , , |
(14)
|
kus
isa mõjude dispersioon mõõdab
¼ kogu aditiivgeneetilisest dispersioonist,
ema mõjude dispersioon sisaldab nii ¼
aditiivgeneetilisest dispersioonist kui ka ühisest
keskkonnamõjust tingitud varieeruvust.
Kõrvutades
esitusi (13) ja (14) võib välja tuua kolm
statistilisest mudelist hinnatavat populatsiooni geneetilist
ja mittegeneetilist determineeritust kirjeldavat parameetrit:
- päritavus,
mis mõõdab aditiivgeneetilise varieeruvuse
osa kogu dispersioonist, on statistilisest mudelist
arvutatav valemiga

(päritavus
arvutatakse enamasti sarnaselt isamudelile vaid
isast tingitud varieeruvuse alusel, emale vastava
dispersiooni arvestamine võib tuua kaasa
päritavuskoefitsiendi nihkega hinnangu mõlemas
veel kõne alla tulevas h2
arvutamise valemis 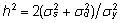 ja
ja  sisaldab lugeja peale geneetilist varieeruvust kajastavate
liikmete
sisaldab lugeja peale geneetilist varieeruvust kajastavate
liikmete 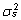 ja
ja  ka püsivast keskkonnamõjust tingitud
dispersiooni, sest vastavalt valemeile (13) ja (14)
ka püsivast keskkonnamõjust tingitud
dispersiooni, sest vastavalt valemeile (13) ja (14)
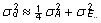 ); );
- ühisest
keskkonnamõjust tingitud varieeruvuse osakaal
koguvarieeruvuses
 on statistilisest mudelist hinnatav suhtena
on statistilisest mudelist hinnatav suhtena
 ; ;
- juhuslikust
keskkonnamõjust tingitud varieeruvuse osakaal
koguvarieeruvuses
 on statistilisest mudelist hinnatav suhtena
on statistilisest mudelist hinnatav suhtena
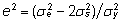 . .
Eeltoodud
definitsioonide põhjal on selge, et h2
+ c2 + e2 = 1.
|