|
Isa
mudeli esitus
Pikki
aastaid oli valdav meetod geneetiliste parameetrite
hindamisel poolõvede analüüs. Selle
analüüsi käigus jagatakse uuritavad
loomad gruppidesse vaid ühe vanema järgi,
teise vanema geneetiline mõju jäetakse
arvesse võtmata (loetakse tühiseks). Et
majanduslikult otstarbekam on valida isasloomi (heade
geenidega isalt on võimalik saada märksa
enam järglasi võrreldes geneetiliselt
potentsiaalilt sama hea emaga), on selleks vaatlusaluseks
vanemaks enamasti isa -- siit ka meetodi enamtuntud
nimetus, isa mudel (sire model). Isa
mudel hindab geneetilise efektina isa mõju,
eeldades vaikimisi, et kõik isad on paaritatud
populatsiooni keskmiste emadega ning emad pole omavahel
sugulased.
Geneetika
mõistes (nn geneetilise mudelina) avaldub
isa j järglase k fenotüübiväärtus
Pjk kujul

mis
on isa mudeli kontekstis esitatav võrrandina
 , , |
(1)
|
kus
MSjk
ja Ejk on vastavalt Mendeli valiku
mõju ja juhuslik keskkonna mõju,
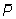 on keskmine fenotüübiväärtus
vaatlusaluses populatsioonis,
on keskmine fenotüübiväärtus
vaatlusaluses populatsioonis,
ASj ja ADij
on vastavalt j. isa aretusväärtus
ja j. isa k. järglase ema aretusväärtus.
Et
huvi pakub vaid isalt järglasel pärandunud
geenide mõju, loetakse kõik ülejäänud
geneetilised efektid kuuluvaks juhuslike keskkonnamõjude
hulka:  . .
Fenotüübiline
dispersioon avaldub vastavalt lineaarsele geneetilisele
mudelile kujul
 , , |
(2)
|
Isa
mudelit rakendades eeldatakse, et nii isade kui ka
emade aretusväärtuste dispersioonid on võrdsed
ning on sestap võrdsed ka kogu populatsiooni
loomade aretusväärtuste dispersiooniga:
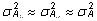 . .
Viimasest
tõdemusest ja valemist (2) lähtuvalt on
kogu aditiivgeneetiline dispersioon 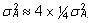 ,
kus ,
kus 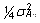 on
isalt järglasele päranduvate geenide summaarsete
mõjude dispersioon (st, et vanemalt järglasele
päranduva geneetilise mõju varieeruvus
on neli korda väiksem, kui vanemate endi geneetiline
varieeruvus) ja ainukese populatsioonigeneetilise
parameetrina isa mudelist leitav päritavuskoefitsient
avaldub suhtena on
isalt järglasele päranduvate geenide summaarsete
mõjude dispersioon (st, et vanemalt järglasele
päranduva geneetilise mõju varieeruvus
on neli korda väiksem, kui vanemate endi geneetiline
varieeruvus) ja ainukese populatsioonigeneetilise
parameetrina isa mudelist leitav päritavuskoefitsient
avaldub suhtena 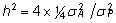 . .
Statistilise
mudelina avaldub isa mudel kujul
 , , |
(3)
|
kus
µ
on populatsiooni keskmine,
Hi on fikseeritud faktori taseme
i mõju (nn karja-aasta-sesooni efekt),
i = 1, ..., p (p on fikseeritud
faktori tasemete arv),
sj on isa j juhuslik mõju
(geneetiline efekt), j = 1, ..., m
(m on isade arv),
eijk on juhuslik viga, k
= 1, ..., N (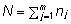 on vaatluste arv, nj on j.
isa järglaste arv; kui järglaste arv kõigil
isadel on n, siis avaldub vaatluste arv kujul
N = n×m).
on vaatluste arv, nj on j.
isa järglaste arv; kui järglaste arv kõigil
isadel on n, siis avaldub vaatluste arv kujul
N = n×m).
Isa
mõju sj eeldatakse olevat
normaaljaotusega keskväärtusega 0 ja dispersiooniga
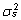 ning juhuslik viga eijk normaaljaotusega
keskväärtusega 0 ja dispersiooniga
ning juhuslik viga eijk normaaljaotusega
keskväärtusega 0 ja dispersiooniga  .
Seega, eeldatakse keskkonna ja genotüübi
sõltumatust, avaldub kogu uuritava tunnuse
dispersioon summana .
Seega, eeldatakse keskkonna ja genotüübi
sõltumatust, avaldub kogu uuritava tunnuse
dispersioon summana
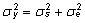 . . |
(3)
|
Kõrvutades
isa mudeli geneetilise esituse (1) statistilise esitusega
(3) ning dispersiooni esituse (2) esitusega (4), on
ilmne, et
- keskmine
fenotüübiväärtus vaatlusaluses
populatsioonis
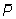 on statistilisest mudelist hinnatav suurusega
on statistilisest mudelist hinnatav suurusega 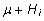 , ,
- statistilisest
mudelist hinnatav isa mõju sj
kujutab enesest hinnangut poolele isa j aretusväärtusest
ASj,
- päritavuskoefitsient
avaldub statistilise mudeli parameetrite kaudu kujul
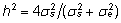 . .
Maatrikskujul
esitatakse isa mudel (3) järgmiselt:
kus
y
on uuritava tunnuse juhuslik N×1 vektor,
b on fikseeritud efektide p×1
vektor,
s on juhuslike isa mõjude m×1
vektor,
e on juhuslike vigade N×1 vektor,
X on fikseeritud efektidele vastav N×p
plaanimaatriks,
Z on juhuslikele efektidele vastav N×m
plaanimaatriks.
Keskväärtused
ja dispersioonimaatriksid defineeritakse kujul:
E(s)
= 0, E(e) = 0, E(y) =
Xb,
 , ,
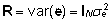 , ,
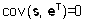
ning
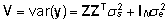 . .
Fakt,
et 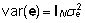 ,
märgib vaatluste sõltumatust (see võib
muutuda, kui ühele loomale vastab mitu mõõtmist)
ning kõigi vaatluste eeldatavalt võrdset
keskkonnatingimustest tingitud varieeruvust. ,
märgib vaatluste sõltumatust (see võib
muutuda, kui ühele loomale vastab mitu mõõtmist)
ning kõigi vaatluste eeldatavalt võrdset
keskkonnatingimustest tingitud varieeruvust.
Keskkonna
ja genotüübi sõltumatus on siin kirjas
kujul 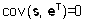 . .
Et
 ,
siis on kõigi geneetiliste efektide dispersioon
ja isade vaheline kovariatsioon on null (isad pole
omavahel sugulased). ,
siis on kõigi geneetiliste efektide dispersioon
ja isade vaheline kovariatsioon on null (isad pole
omavahel sugulased).
|