Aretusväärtuste hindamine isa mudelist

Vastavalt isa mudeli definitsioonile on selle alusel võimalik hinnata vaid isa mõju. Eeldusel, et järglaste fenotüübiväärtuste erinevust põhjustavad mittegeneetilised efektid on arvesse võetud ja valikut emade osas ei ole toimunud, on isa mudelist hinnatava isa mõju näol tegu isalt järglasele pärandunud geenide summaarse mõjuga, mis moodustab poole isa aretusväärtusest. Sageli ei esitatagi poolõvede mudeli tulemusena mitte looma kogu aretusväärtust, vaid üksnes selle mudelist hinnatavat osa, so järglasele päranduvat geneetilist efekti (inglise keeles transmission ability).

BLUP-hinnangud isa mõjule, arvestades karja-aasta-sesooni efekti, on maatriksvõrdusena leitavad Hendersoni segamudeli võrrandist

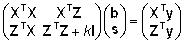,	(6)
kus
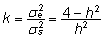,	(7)

sest 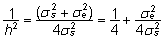, millest .

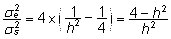Isa j aretusväärtuse a_j hinnangon leitav valemist (6) saadud isa mõju hinnangu 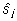kaudu:

.

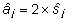Juhul, kui päritavuskoefitsiendi väärtus h² pole teada, asendatakse selle väärtus valemis (6) hinnanguga 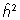, mis on leitud statistilisest mudelist hinnatud dispersioonikomponentide kaudu:

.

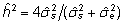Näide. Lehmade piimatoodangut on mõõdetud kahes erinevas karjas. Kõik mõõtmised on tehtud samal aastal ja kõik vaadeldud lehmad on ühevanused. Lisaks karjale, kuhu lehm kuulub, on teada ka tema isa. Ülesandeks on hinnata isade aretusväärtust, kasutades isa mudelit. Piimatoodangu päritavuseks võib lugeda 0,25.

Andmetabel on järgmine:

Lehm	Isa	Kari	Piimatoodang
101	1	1	7000
102	2	1	6600
103	3	1	6800
104	3	1	7200
201	2	2	8000
202	2	2	8300
203	3	2	8900

Mudel sisaldab karja mõju kui fikseeritud efekti ning isa mõju kui juhuslikku efekti:

, .

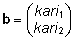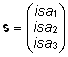Lahendite ühesuse huvides loeme mudeli vabaliikme võrdseks nulliga. Plaanimaatriksid X ja Z, mis seovad iga vaatluse talle mõjuvate faktorite tasemetega, on

, .

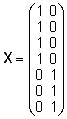Faktorite mõjude hindamiseks paneme esmalt kirja mudelile vastavad vähimruutude võrrandid ning liidame seejärel segamudeli võrrandite saamiseks isamõjule vastavaile diagonaalielementidele dispersioonide suhte k. Näiteandmetele vastavad vähimruutude võrrandi kordajate maatriks ja vabaliikmete vektor on

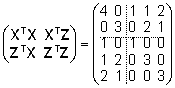ja .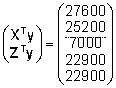

Päritavuskoefitsient h² = 0,25 ning seega 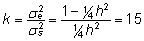. Faktorite mõjude hinnangud on nüüd leitavad segamudeli võrrandist

.

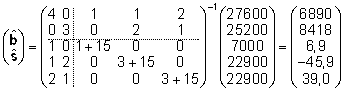Esimese isa aretusväärtuse hinnang on 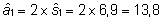; teisel isal 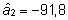ja kolmandal isal .

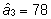Märkus. Et vastavalt juhuslike efektide olemusele võrdub nende keskväärtus nulliga, siis võrduvad nulliga ka isade keskmine mõju ja isade aretusväärtuste summa.
Antud näite korral .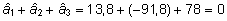

Küsimus. Nii teise kui ka kolmanda isa tütarde summaarne toodang on 22900 kg. Miks on aga nende hinnatud aretusväärtused nii erinevad?

Kui kõigi analüüsitavate isade järglased on pärit sarnastest keskkonnatingimustest või on fenotüübiväärtused analüüsi eelselt mittegeneetiliste mõjude suhtes korrigeeritud, lihtsustub mudel (3) kujule

.

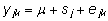Isa j mõju hinnang avaldub taolise mudeli puhul vastavalt üldiste lineaarsete mudelite teooriale kujul

,

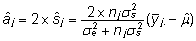(8)

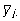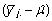kus on j. isa järglaste keskmine fenotüübiväärtus ja n_j on järglaste arv. Et suurus kujutab enesest j. isa järglaste keskmist erinevust populatsiooni/karja keskmisest ning selle erinevuse kordaja on tänu seosele (7) teisendatav kujule

,

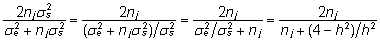avaldub j. isa aretusväärtus tema järglaste keskmise fenotüübiväärtuse kaudu valemiga

.

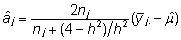Saadud tulemus on identne selektsiooniindeksiga hindamaks isa aretusväärtust tema järglastel mõõdetud fenotüübiväärtuste alusel. Seega on tehtud eeldustel (keskkonnamõjude puudumine) selektsiooniindeksi kujul leitud aretusväärtuste parimad lineaarsed prognoosid (BLP) identsed üldisest lineaarsest mudelist leitud aretusväärtuste parimate lineaarsete nihketa prognoosidega (BLUP).