|
|
Kreutzwaldi 62, A-213
|
|
Õpiobjektid -> Indiviidide vaheline
aditiivgeneetiline sugulus
INDIVIIDIDE VAHELINE ADITIIVGENEETILINE SUGULUS
|
|
|
|
WRIGHT'I RAJAKOEFITSIENTIDE MEETOD |
|
|
|
|
|
|
WRIGHT'I
RAJAKOEFITSIENTIDE MEETOD SUGULUSKOEFITSIENTIDE LEIDMISEKS -> NÄITED
Näide
1. Leiame alljärgnevalt toodud põlvnemisskeemist
indiviidi O inbriidingukoefitsiendi.
Indiviidi
O vanemad X ja Y omavad ühiseid esivanemaid
W ja Z, viimastest W on omakorda saadud
sugulusaretuse tulemusel. Vastavalt valemile (7) tuleb FO
arvutamisel leida päritolult identsete alleelide tõenäosus
kahest põlvnemisteest lähtudes ja saadud tulemused
liita:
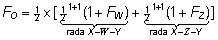 . .
Et
FZ = 0 ja
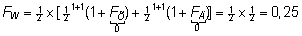
(vaikimisi
eeldame, et indiviidid Õ, Ä ja Z
pole omavahel suguluses), siis
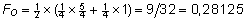 . .
|
|
Suguluskoefitsiendi
leidmise näitena uurime indiviidide X ja O vahelist
aditiivgeneetilist sugulust. Et indiviididel X ja O
on kaks ühist eellast - W ja Z, ning lisaks on
indiviid X indiviidi O vanemaks, siis avaldub nendevaheline
aditiivgeneetiline sugulus kolme liidetava summana:
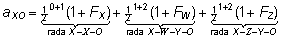 . .
Et
FX = fWZ = 0, FW
= ¼ ja FZ = 0 siis 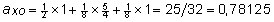 . .
Keerulisemate
põlvnemisskeemide puhul on sugulus- ja inbriidingukoefitsientide
arvutamisel Wright'i rajakoefitsientide meetodil mõttekas esitada
arvutused tabelina, kus on kirjas kõik võimalikud mittekattuvad
rajad ühise eellaseni ja neile vastavad liidetavad koefitsiendi
arvutusvalemis.
Näide
2. Kõrvaloleval joonisel on kujutatud osa Egiptuse Uuele
riigile aluse pannud vaaraode 18. dünastia (1552 e.m.a.)
sugupuust. Leiame kuninganna Hatšepsuti ja vaarao Thutmosis
II tütre Neferura inbriidingukoefitsiendi, jättes
arvesse võtmata vaarao Thutmosis I spekulatiivse pärinemise
(joonisel katkendlikud jooned).
Arvutused
koondame alljärgnevasse tabelisse.
| Tee |
nij
+ mij
|
Fi
|
FP
liidetav
|
| LKM |
2
|
0
|
|
| LHEIM |
4
|
FE
= ¼
|
|
| LHFIM |
4
|
FF
= ¼
|
|
| LHECFIM |
6
|
0
|
|
| LHFCEIM |
6
|
0
|
|
| LHFDEIM |
6
|
0
|
|
| LHEDFIM |
6
|
0
|
|
| LHECADFIM |
8
|
0
|
|
| LHEDACFIM |
8
|
0
|
|
| LHFCADEIM |
8
|
0
|
|
| LHFDACEIM |
8
|
0
|
|
| LHECBDFIM |
8
|
0
|
|
| LHEDBCFIM |
8
|
0
|
|
| LHFCBDEIM |
8
|
0
|
|
| LHFDBCEIM |
8
|
0
|
|
|
|
Kui alleelide
pärimisteed lõikuvad (lõikepunktis on ühine
eellane), siis tuleb trajektoor sellest ühisest eellasest ettepoole
(ülespoole) arvestusest välja jätta.
Näide
3. Analüüsime põlvnemispuud kõrvaloleval
joonisel, leides indiviidi Z inbriidingukoefitsiendi.
Indiviidi Z vanemate, X ja Y, ühised
eellased on A, B, C ja H (on ka
D, aga põlvnemistee temani kulgeb nii X-i
kui ka Y-i puhul läbi ühise eellase H,
mistõttu alleelide põlvnemine seda teed mööda
on juba arvesse võetud).
Koondame
arvutused alljärgnevasse tabelisse.
| Tee |
nij
+ mij
|
Fi
|
FZ
liidetav
|
| XKHLY |
2
|
FH
= 1/8
|
|
| XKGCHLY |
4
|
0
|
|
| XKHDBELY |
4
|
0
|
|
| XKHDBEJMY |
8
|
0
|
|
| XKGCADHLY |
8
|
0
|
|
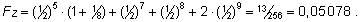
|
|
|
|
|





