Geodeetiline otseülesanne on koordinaatide juurdekasvude ja koordinaatide arvutamine. Koordinaatide juurdekasvud leitakse joone pikkuse ja direktsiooninurga järgi. Geodeetiline pöördülesanne on direktsiooninurga ja joone horisontaalprojektsiooni leidmine joone otspunktide ristkoordinaatide järgi. Järgnev näidisülesanne sisaldab endas otse- ja pöördülesande.

Näidisülesanne: On antud kahe geodeetilise alusvõrgu punkti A ja B ristkoordinaadid X_A, Y_A ja X_B,Y_B. Leida punkti C ristkoordinaadid X_C ja Y_C, kui on teada punkti C kaugus punktist B, so S_BC ja mõõdetud vasakpoolne nurk punktis B- so λ_B= 93°03’10”
Antud:
X_A = 5057,17 m
Y_A = 4863,61 m
X_B = 5007,08 m
Y_B = 4755,59 m
λ_B= 93°03’10”
S_BC = 177,71 m
Leida: X_C ja Y_C
X_C = X_B+S_BC×cos α_BC
Y_C = Y_B+S_BC×sin α_BC
α_BC = α_AB - 180°+λ (vasakpoolsed nurgad)
α_BC = α_AB + 180°-β (parempoolsed nurgad)
1. Punkti C koordinaatide leidmine.

Kõigepealt tuleb leida joone BC direktsiooninurk. Selleks arvutatakse kõigepealt joone AB juurdekasvud:

Δx_AB = X_B-X_A = 5007,08-5057,17 = -50,09 m
Δy_AB = Y_B-Y_A = 4755,59 - 4863,61 = -108,02 m

Joone AB rumbi arvutuse puhul on nii Δx kui ka Δy miinus märgiga ja see tähendab et meil on tegu kolmanda veerandi joonega (joonis 1.). Sellest tulenevalt tulebki rumbile liita juurde 180°, siis saame joone direktsiooninurga.
α_AB=180°+R_AB = 180°+65°07’20” = 245°07’20”
α_BC = α_AB-180°+λ=245°07’20”-180°00’00”+93°03’10”=158°10’30”
X_C= 5007,08 + 177,71×cos 158°10’30” = 5007,08+(-164,97)= 4842,11 m
Y_C=4755,59+177,71×sin 158°10’30”=4755,59+66,07=4821,66 m

2. Kontroll: α_BC leidmine

Joone BC rumbi arvutuse puhul on Δx miinus märgiga ja Δy on positiivne ja see näitab et see joon on II veerandis. Sel juhul tuleb joone BC direktsiooninurga saamiseks 180°-st lahutada rumbi väärtus.

α_BC= 180°-R = 180°- 21°49’33”= 158°10’27”

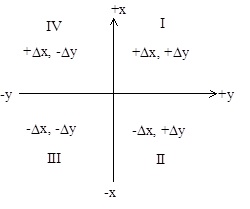
Joonis 1. Juurdekasvude märgid erinevates veerandites

Joonisel 2 on näidatud joonte AB ja BC direktsiooninurgad ja rumbid.

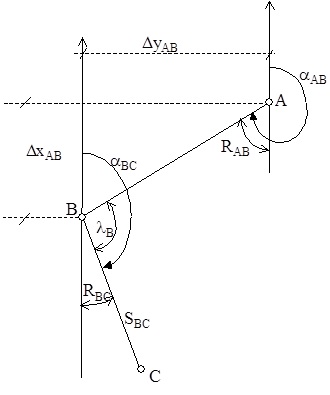
Joonis 2. Joonte direktsiooninurgad