|
Karp-vurrud
diagramm, variant 2
(erinditega)
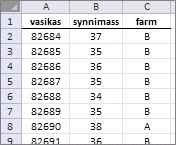 Andmed. Andmed.
Näiteandmestik sisaldab 68 neljast erinevast
farmist pärit vasika sünnimasse; andmed
võite katsetamiseks alla laadida siit:
vasikas.xls.
Ülesanne.
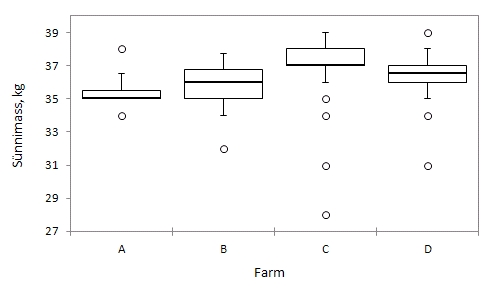
Konstrueerida karp-vurrud diagrammid vasikate sünnimassidele
farmide kaupa, esitades erandlikud väärtused
eraldi punktidena.
Probleem.
Exceli joonisetüüpide hulgas antud
diagrammi ei ole.
Lahendus.
- Arvutada
farmide kaupa mediaan ja kvartiilid,
- tekitada
abitabel erandlikest väärtustest (jällegi
farmide kaupa),
- leida
mediaanide-kvartiilide tabelisse lisaks minimaalsed
ja maksimaalsed väärtused, jättes
kõrvale erinditeks loetud väärtused,
- konstrueerida
mediaanide-kvartiilide tabeli alusel abitabel joonisel
esitatavate andmetega,
- joonistada
tulpdiagramm,
- modifitseerida
viimast, saamaks joonisele karp-vurrud diagrammi
väljanägemist,
- lisada
joonisele punktidena erandlikud väärtused.
Tööjuhend.
1)
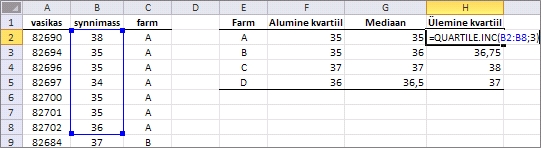
Esimese sammuna tuleb konstrueerida abitabel ning
arvutada sinna farmide kaupa alumised ja ülemised
kvartiilid ja mediaanid.
Selleks
tuleks andmestik sorteerida farmi järgi ning
rakendada arvkarakteristikute arvutamiseks vastavaid
funktsioone (kõik kolm joonise tegemiseks vajalikku
suurust on leitavad näiteks funktsiooniga QUARTILE.INC
(vanemais Exceli versioonides funktsioon QUARTILE),
mille teise argumendi väärtus määrab
ära arvutatava suuruse: 1 alumisele kvartiilile,
2 mediaanile jne).
2)
Järgmise sammuna tuleb iga farmi tarvis leida
piirid erandlike väärtuste tarvis (mis arvust
alates lugeda sünnimass erandlikuks).
Küllaltki
standardne variant (mida näiteks statistikapakett
R vaikimisi rakendab) on lugeda erandlikeks
alumisest/ülemisest kvartiilist enam kui 1,5-kordse
kvartiilide vahe võrra väiksemad/suuremad
väärtused.
Piirid
erandlike väärtuste tarvis võib esitada
jällegi tabelina:

(tähistustes
IQR - Inter Quartile Range (kvartiilide vahe), LQ
- Lower Quartile (alumine kvartiil), UQ - Upper Quartile
(ülemine kvartiil)).
3)
Erandlikest väärtustest lisatabeli tegemiseks
on mõttekas kasutada Exceli nn täpsemat
filtrit (Advanced Filter), mis toimib analoogselt
kuitahes suurte andmetabelite korral.
Algse
andmetabeliga identsete veerunimedega abitabelisse
(Advanced Filter'i argumenttabelisse) tuleb
trükkida tingimused, millele vastavaid ridu algsest
andmetabelist välja filtreerida soovitakse, seejuures
tuleb tingimused, mis peavad korraga kehtima, trükkida
ühte ritta, üksteise suhtes alternatiivsed
tingimused (kas see või teine) tuleb trükkida
eraldi ridadesse.
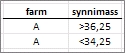 Näiteks
paremal toodud abitabel käseb Excelil
välja otsida kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass on suurem kui 36,25
kg pluss kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass on väiksem kui
34,25 kg. Näiteks
paremal toodud abitabel käseb Excelil
välja otsida kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass on suurem kui 36,25
kg pluss kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass on väiksem kui
34,25 kg.
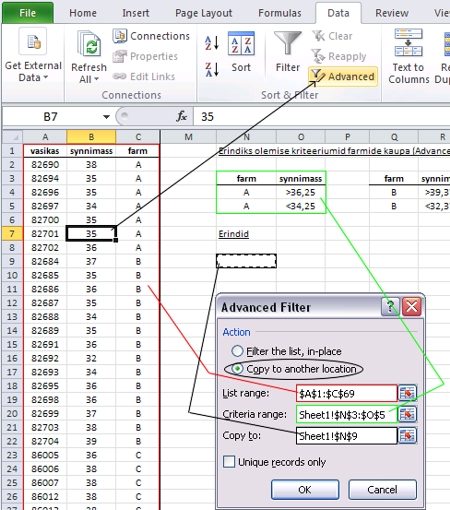
Rakendades täpsemat filtrit, kopeerimaks lisatabelisse
farmi A kuuluvaid erandlike sünnimassidega vasikaid,
tuleb (vt ka järgnevat skeemi)
- esmalt
anda ette algtabel (või osa sellest), millest
tingimustele vastavaid ridu otsida (koos pealkirjareaga!),
- teisena
anda ette filtreerimiskriteeriumeid sisaldava abitabeli
asukoht (jälle koos pealkirjareaga!) ning
- kolmandana
käskida Excelil kopeerida välja
filtreeritud tabeli read (koos pealkirjadega) uude
tabelisse ja anda ette loodava tabeli vasaku ülemise
nurga asukoht.
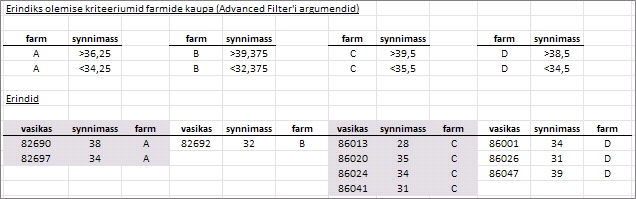
Pannes
kirja filtreerimistingimused kõigi nelja farmi
tarvis ning rakendades Advanced Filter't neli
korda, on tulemuseks lisatabelid erandlikest väärtustest
farmide kaupa:
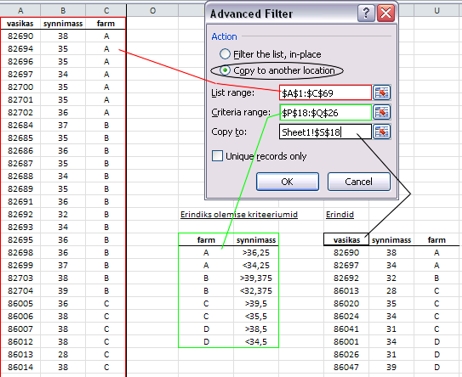
Muidugi võib kõigi farmide erandlikud
väärtused välja filtreerida ka korraga,
andes filtreerimistingimused ette ühe tabelina:
4)
Edasi tuleks lisada mediaanide-kvartiilide tabelisse
minimaalsed ja maksimaalsed väärtused, jättes
kõrvale erinditeks loetud väärtused.
Selleks
võib tekitada abitabelid mitteerandlikest väärtustest,
kasutades Advanced Filter'i abi (soovitatav
hästi suure hulga erindite korral), ning leida
minimaalsed ja maksimaalsed väärtused sealt.
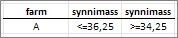 Näiteks
paremal toodud abitabel käseb Advanced Filter'l
välja otsida kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass jääb lõiku
[34,25 kg; 36,25 kg]. Näiteks
paremal toodud abitabel käseb Advanced Filter'l
välja otsida kõik vasikad, kes on sündinud
farmis A ja kelle sünnimass jääb lõiku
[34,25 kg; 36,25 kg].
Kui
erindeid on vähe, siis võib kokku lugeda,
kui mitu neist on alumisest kvartiilist väiksemad,
ning kasutada ülejäänud väärtustest
vähima leidmiseks funktsiooni SMALL ning analoogselt
mitteerandlikest väärtustest suurima leidmiseks
funktsiooni LARGE.
Näiteks kui alumisest kvartiilist väiksemaid
erindeid on kaks, siis väljastab ülejäänud
väärtustest minimaalse väärtuse
funktsioon SMALL teise argumendiga 3 (väiksemate
väärtuste poolt kolmas väärtus
algsest andmetabelist, sest kaks vähimat olid
erandlikud).
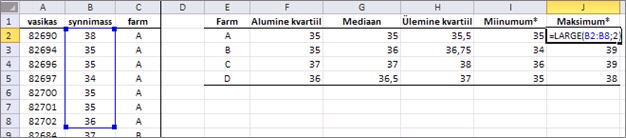
Täiendades mediaanide-kvartiilide tabelit minimaalsete
ja maksimaalsete väärtustega ilma erinditeta,
on tulemus järgmine:
5)
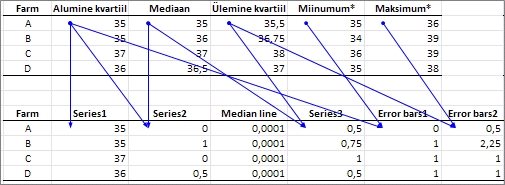
Järgmise sammuna tuleb leitud arvkarakteristikute
tabeli alusel konstrueerida uus, Excelis loodavale
tulpdiagrammile aluseks olev tabel:

Veerud
uues tabelis on püütud nimetada vastavalt
nendes olevate arvude rollile loodavas joonises. Seejuures
(vt ka järgnevat joonist)
- 'Series1'
= 'Alumisne kvartiil' (need arvud vastavad esimese
tulba kõrgusele tulpdiagrammil e karbi alumisele
servale karp-vurrud diagrammil);
- 'Series2'
väärtused on arvutatud kui 'Mediaan -
Alumine kvartiil' (see suurus määrab ära
teise tulba kõrguse tulpdiagrammil e mediaanile
vastava joone karp-vurrud diagrammil);
- veerg
'Median line' ei ole ilmtingimata vajalik, vaja
on seda siis, kui soovitakse esitada mediaanile
vastavat joont graafikul paksemana, selle veeru
väärtusteks peaks olema väga väikesed
positiivsed arvud (näiteks 0,0001);
- 'Series3'
väärtused on arvutatud kui 'Ülemine
kvartiil - Mediaan' (see suurus määrab
ära kolmanda tulba kõrguse tulpdiagrammil
e karbi ülemise serva karp-vurrud diagrammil);
- 'Error
bars1' väärtused on arvutatud kui 'Alumine
kvartiil - Miinimum*' (selle suuruse alusel joonistatakse
'Series1'-le vastavale tulbale alumine veajoon,
mis karp-vuurud diagrammi mõistes tähendab
joont alumisest kvartiilist minimaalse väärtuseni);
- 'Error
bars2' väärtused on arvutatud kui 'Maksimum*
- Ülemine kvartiil' (selle suuruse alusel joonistatakse
'Series3'-le vastavale tulbale ülemine veajoon,
mis karp-vuurud diagrammi mõistes tähendab
joont ülemisest kvartiilist maksimaalse väärtuseni).
6)
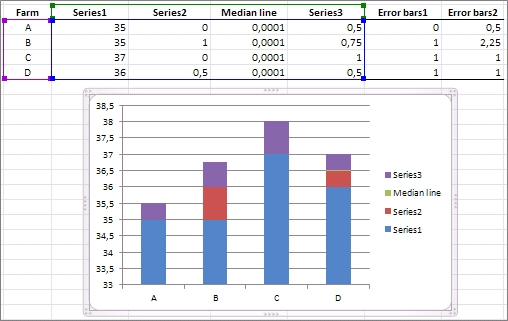
Uue abitabeli veergude 'Series1'-'Series3' alusel
tuleb konstrueerida tulpdiagramm, kus tabeli veerud
vastaksid erinevatele andmeseeriatele
(vajadusel tuleb Exceli vaikimisi genereeritud joonisel
read ja veerud ära vahetada).
7)
Saadud joonisel tuleb (täpsemaid juhiseid võib
vaadata tavalise karp-vurrud diagrammi konstrueerimise
õpetusest)
- lisada
'Series1' tulbale alumine veajoon veerus
'Error bars1' olevate väärtuste alusel
ning 'Series3' tulbale ülemine veajoon
veerus 'Error bars2' olevate väärtuste
järgi;
- kaotada
ära nii sisu kui ka piirjooned 'Series1'
tulbalt ning sisu 'Series2' ja 'Series3'
tulpadelt (lisades vajadusel viimastele piirjooned).
- Lisaks
on soovitatav
-
esitada mediaanile vastav joon paksemana, värvides
selleks vastava andmeseeria tulba piirjooned
mustaks;
-
kaotada ära legend ja horisontaalsed ruudujooned,
-
lisada telgedele nimed,
-
vähendada tulpade (karp-vurrud diagrammide)
vahelist kaugust (Gap Width), st et vähendada
tühja ebainformatiivset ala joonisel,
- …
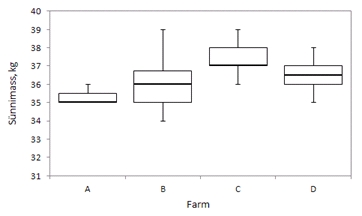
Tulemus:
 8)
Joonisele erandlike väärtuste punktidena
lisamiseks tuleb 8)
Joonisele erandlike väärtuste punktidena
lisamiseks tuleb
- esmalt
tekitada erandlikest väärtustest ühine
tabel (kui seda ei ole juba tehtud kõigi
erandlike väärtuste korraga välja
filtreerimise teel) ning
- lisada
tabelisse sünnimasside ette igale farmile
oma arvuline kood, seejuures peavad arvulised
koodid olema võrdsete vahedega (näiteks
1, 2, 3, 4 või 1, 3, 5, 7).
9)
Farmikoodide ja sünnimasside veerud tuleb lisada
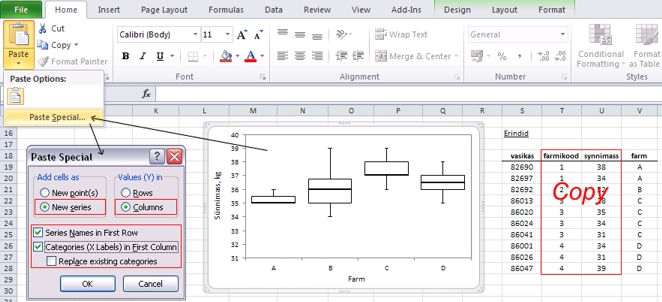
loodud joonisele uute andmeseeriatena. Lihtsaim viis
selleks on
- võtta
vastavad veerud blokki ja kopeerida arvuti vahemällu,
- seejärel
klikkida joonisel ning kleepida käsu Paste
Special abil joonisele kui uued andmeseeriad
(vt joonist).
Tulemus:
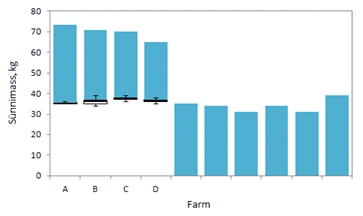
10)
Edasi tuleb Excelile öelda, et uute lisatud
andmeseeriate alusel tuleb joonistada hoopis punktdiagramm:
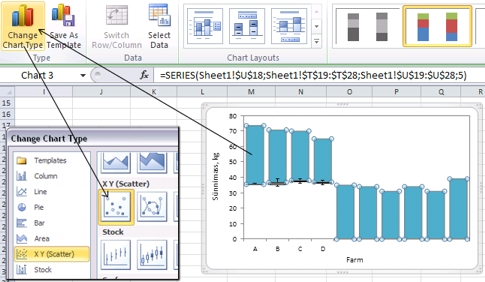
Tulemus:
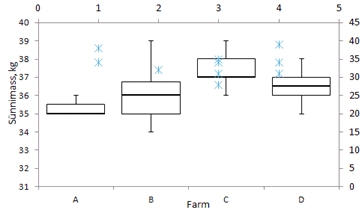
11)
Viimase sammuna tuleb
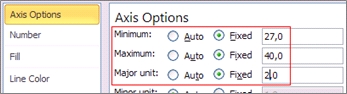 määrata
mõlemale vertikaalsele teljele sama
ulatus (lähtudes minimaalsest ja maksimaalsest
väärtusest - näiteks antud ülesande
puhul võiks ulatuseks olla 27-40, sest minimaalne
sünnimass on 28 kg ja maksimaalne 39 kg; määrata
mõlemale vertikaalsele teljele sama
ulatus (lähtudes minimaalsest ja maksimaalsest
väärtusest - näiteks antud ülesande
puhul võiks ulatuseks olla 27-40, sest minimaalne
sünnimass on 28 kg ja maksimaalne 39 kg;
- muuta
teise horisontaaltelje skaalat nii, et selle
alusel joonisele paigutatavad erindid satuksid erinevatele
farmidele vastavate diagrammidega samale vertikaalsele
joonele;
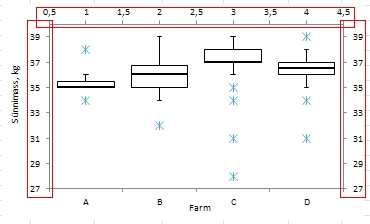
- kaotada
ära ühikud ja märgendid teiselt horisontaal-
ja teiselt vertikaalteljelt ning muuta erindite
tähistamiseks kasutatav sümbol sobivamaks.
Tulemus:

|