Tõenäosuspaber (quantile-quantile plot)

Tõenäosuspaberit (quantile-quantile plot, qq-plot, normal probability plot) kasutatakse, võrdlemaks uuritava tunnuse (valimi) jaotust normaaljaotusega (tavaliselt; sama metoodika on kasutatav ka teostamaks võrdlust teiste teoreetiliste jaotustega).

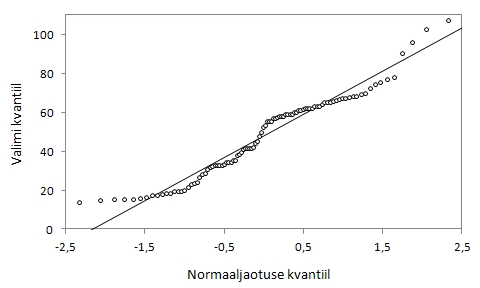
Joonise tarvis moodustatakse valimi kvantiilidest* ja (standardse) normaaljaotuse vastavatest kvantiilidest punktipaarid. Punktid kantakse graafikule ja juhul, kui uuritav tunnus on ka tegelikult normaaljaotusega, peaksid kõik punktid jääma enam-vähem ühele sirgele. Kui punktid kipuvad sirgest märgatavalt kõrvale kalduma, siis pole kardetavasti tegemist normaaljaotusega. Selgema võrdlemise huvides kantakse mõnikord graafikule ka joon, mis vastab täpselt normaaljaotuse järgi jaotuvatele andmetele (valimist leitud keskmise ja standardhälbega).

*Kvantiil e protsendipunkt e protsentiil on väärtus, millest väiksemaid väärtusi esineb vaid antud tõenäosusega (näiteks 0,5-kvantiil on mediaan).
 

Andmed.
Näiteandmestik sisaldab 223 angerja pikkuseid (lisaks ka püügikoha andmeid, aga neid antud joonise tegemisel ei kasutata; andmed võite katsetamiseks alla laadida siit:

angerjas.xls.
 

Ülesanne.
Joonistada tõenäosuspaber angerjate pikkusele.

Probleem.
Exceli joonisetüüpide hulgas antud diagrammi ei ole.
 

Lahendus.

• Teha Exceli töölehele abitabel tõenäosustest 0,01-st 0,99-ni sammuga 0,01, arvutada sinna järele valimi vastavad protsendipunktid ja standardse normaaljaotuse kvantiilid ning kanda neist moodustuvad punktipaarid punktdiagrammina graafikule;
• arvutada ideaaljuhule (normaaljaotus) vastava sirge otspunktid - tõenäosustele 0,001 ja 0,999 vastavad standardse normaaljaotuse kvantiilide ning andmetest leitud keskmise ja standardhälbega normaaljaotuse kvantiilide punktipaarid - ja joonistada nende alusel graafikule sirge.
   

Tööjuhend.

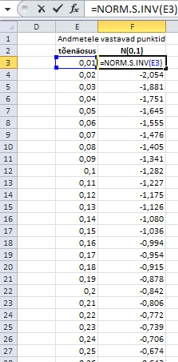
1) Esmalt tuleb teha Exceli töölehele abitabel tõenäosustest 0,01-st 0,99-ni sammuga 0,01 ja arvutada sinna järele funktsiooniga NORM.S.INV (Excel 2003-s ja vanemais versioonides funktsioon NORMSINV) standardse normaaljaotuse kvantiilid.

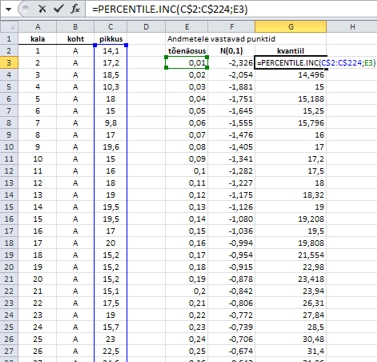
Teine etapp on leida standardse normaaljaotuse kvantiilide kõrvale funktsiooniga PERCENTILE.INC (Excel 2003-s ja vanemais versioonides funktsioon PERCENTILE) vastavad valimi kvantiilid (protsendipunktid).

 + 
 

2) Järgnevalt tuleb leitud standardse normaaljaotuse kvantiilide ja valimi kvantiilide alusel konstrueerida punktdiagramm.

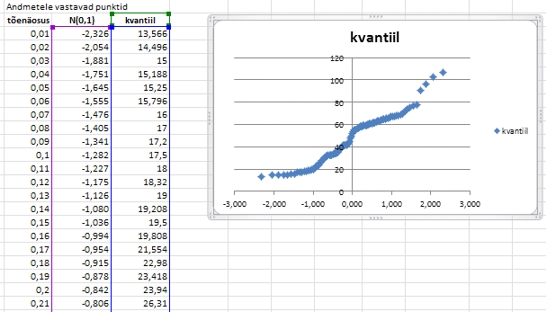
3) Kuigi saadud joonise kujundust võib ka kohe muutma hakata, on ehk mõttekam lisada enne joonisele veel ka ideaaljuhule (normaaljaotus) vastav sirge.

• Selleks tuleb esmalt arvutada sirge otspunktid - tõenäosustele 0,001 ja 0,999 vastavad standardse normaaljaotuse kvantiilid (funktsiooniga NORM.S.INV) ja andmetega sobiva normaaljaotuse kvantiilid (funktsiooniga NORM.INV, Excel 2003-s ja vanemais versioonides NORMINV; keskmise ja standardhälbena tuleb ette anda valimist leitud vastavate parameetrite hinnangud).

• Ja edasi tuleb lisada uus kahest punktist koosnev andmeseeria graafikule.

  
   

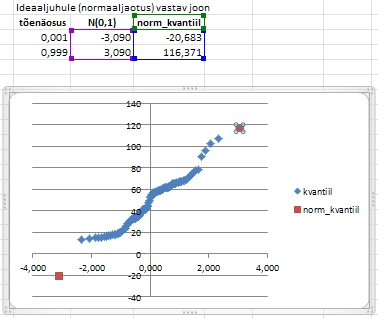
4) Viimase etapina tuleb viia joonis sobivale kujule:

• lisada normaaljaotusele vastavate punktide vahele sirge ja kaotada vastavate punktide märgendid;
• muuta valimi kvantiilidele vastavate punktide kujundust (näiteks võiks need muuta mustade piirjoontega seest valgeteks ringideks suurusega 3);
• kaotada jooniselt legend ja ruudujooned;
• määrata x-telje ulatuseks vahemik -2,5-st 2,5-ni ning y-telje ristumiskohaks väärtus -2,5;
• määrata y-telje ulatuseks vahemik 0-st 110-ni (sest angerjas ei saa olla alla 0 cm pikk ja maksimaalne angerjate pikkus antud andmestikus on 108 cm);
• lisada telgedele nimed ning sisemisele diagrammialale piirjoon, kaotades samas ära kogu joonist ümbritseva piirjoone.

Ja ongi valmis.