2.1. Lahendada geodeetiline pöördülesanne, s.t. leida määratud joonte otspunktide ristkoordinaatide järgi joonte pikkused ja võrrelda arvutatud joonepikkusi laboratoorses töös nr. 1 mõõdetud joonepikkustega.

Pöördülesandeks nimetatakse joonte horisontaalprojektsioonide ja direktsiooninurkade (rumbide) leidmist joonte otspunktide ristkoordinaatide järgi (joonis 1.). Laboratoorses töös nr. 2 ülesandes 1 on määratud kolmele punktile ristkoordinaadid. Ristkoordinaatide järgi saab leida joonte pikkused. Selleks tuleb joonisel 1 toodud valemisse (s₁₂) sisestada joone otspunktide koordinaadid ja leida joone pikkus. Analoogselt arvutatakse ka joone s_{23 ja} s₃₁ pikkus.

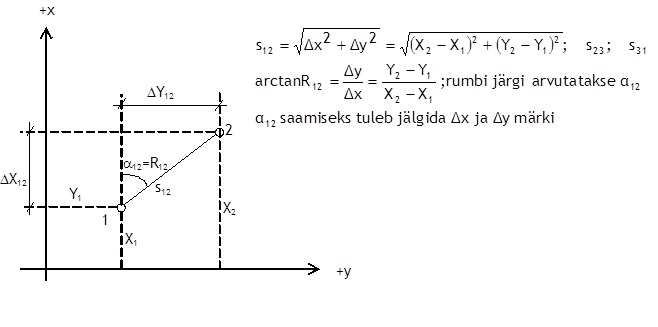
Joonis 1. Geodeetilise pöördülesande lahendamine

Näide horisontaalprojektsiooni arvutamise kohta ristkoordinaatide järgi.

Antud on kahe punkti ristkoordinaadid (tabel 1.).

Tabel 1. Punktide ristkoordinaadid (km)

	X	Y
1	6541,950	641,650
2	6540,700	643,345

Joonisel 1 toodud valemi järgi (s₁₂) saab arvutada joone 1-2 horisontaalprojektsiooni.

Arvutatud horisontaalprojektsioon tuleb kanada tabelisse 2.

2.2. Punktide geodeetiliste koordinaatide järgi saab arvutada joonte pikkused selle ülesande lõppu lisatud veebilehel. Seal saad sisestada oma punktide geodeetilised koordinaadid ja nende järgi arvutatakse punktidevaheline kaugus.

Andmete sisestamise järjekord veebilehel:

1. Ellipsoidi valik on GRS-80. Kuna meie teeme mõõtmised kaardilehel 1:50 000 ja selle koostamisel on kasutatud ellipsoidi GRS-80 parameetreid, siis tuleb ka siin valida sama ellipsoid. Ekvatoriaalraadius on 6378137,000 m ja polaarraadius on 6356752,3141m (need võib jätta ka sisestamata).

 

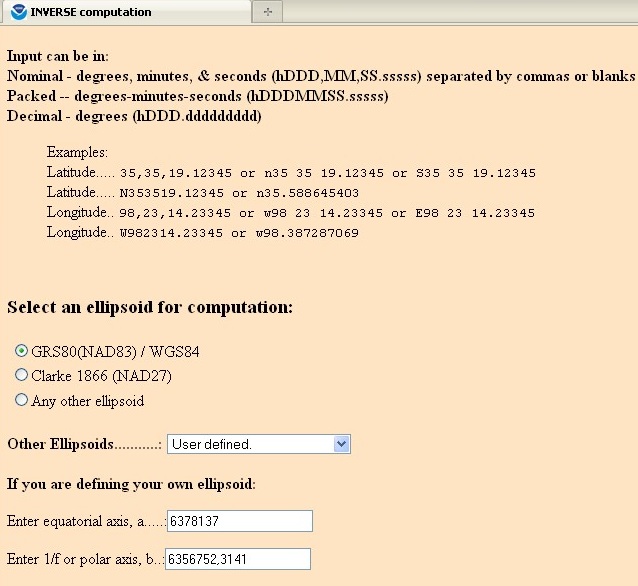
Kui oled ellipsoidi valinud, siis saad sisestada oma joone 1-2 ühe otspunkti nr (1) ja tema põhjalaiuse ja idapikkuse. Seejärel sisesta punkti 2 põhjalaius ja idapikkus. Geodeetiliste koordinaatide sisestamisel võid kraadide, minutite ja sekundite eraldamiseks kasutada nii tühikut kui ka koma. Allpool toodud näites on punkti 1 puhul kasutatud ühikute eraldamiseks koma ja punkti 2 puhul tühikut.

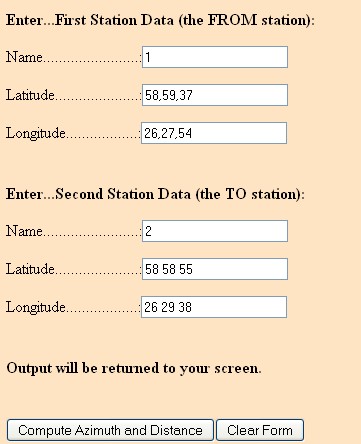
Peale koordinatide sisestamist vajuta lehe all olevale ristkülikule- arvuta pikkus ja asimuut Se.

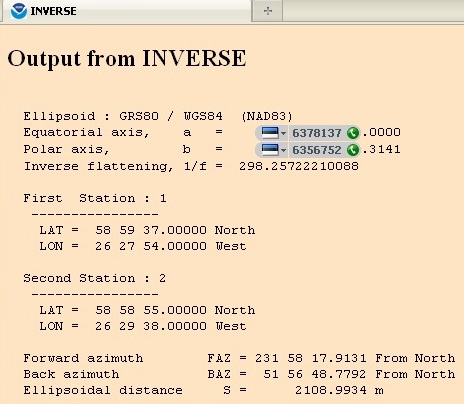
Arvutuste protokollis on näha juba joone 1-2 arvutatud pikkus S= 2108,9934 m= 2109 m, mille saab kanda võrdlustabelisse 2.

Tabel 2. Mõõdetud ja arvutatud pikkuste võrdlus

Joon	Plaanilt mõõdetud Smõõd (m)	Ristkoordinaatide järgi arvutatud Sarvut (m)	Geodeetiliste koordinaatide järgi arvutatud Se (m)	Smõõd- Sarvut (m)	Smõõd- Se (m)
1-2	2115	2106	2109	9	6
2-3
3-1

Lubatud erinevus on: S_mõõd-S_arvut = ΔS_1-2 ≤ 4m

Plaanilt mõõdetud joonepikkuse ja plaanilt mõõdetud joone otspunktide koordinaatide järgi arvutatud joonepikkuste täpsused ja lubatavad erinevused.

1. Plaanilt vahetult mõõdetud joonepikkuse täpsus võrdub tema otspunktide asendi määramise täpsusega. Prof. A. Maslovi järgi on see m_s= ± 0,08 mm.
2. Plaanilt graafiliselt määratud ristkoordinaatide järgi arvutatud joonepikkuse määramise täpsus:

kus m_k=m_x=m_y on joone otspunkti abstsissi (x) või ordinaadi määramise täpsus.
Näiteks Drobõševi joonlauaga konstrueeritud koordinaatvõrgu puhul on m_k= ± 0,11 mm ja m_s′= 0,16 mm. Järelikult vahetult mõõtes saab joone pikkuse plaanil määrata kaks korda täpsemini kui graafiliselt määratud koordinaatide järgi arvutades.
Joonepikkuse lubatava vea ΔS võime võtta võrdseks täpsuse kahekordse väärtusega, s.t. ΔS = 2m_s
1:50 000 mõõtkavas plaanil võime seega kahel erineval viisil saadud joonepikkuste lubatavaks erinevuseks võtta
ΔS = 2×m_s×M = 2×0,08×50000 = 2×4 = 8 m, kus M on mõõtkava nimetaja.

 

Kui sisestad allpool olevale veebilehele oma punktide geodeetilised koordinaadid siis saad teada punktidevahelised kaugused. Need kanna tabelisse 2 neljandasse veergu.