|
|
Andmeanalüüs
MS Exceli abil
|
Funktsioon
CORREL(array1,array2)
Lihtsaim viis pidevate arvtunnuste
vahelise lineaarse seose iseloomustamiseks on korrelatsioonanalüüs.
Lineaarne korrelatsioonikordaja on MS
Exceli keskkonnas leitav funktsiooniga CORREL(array1,array2),
kus array1 ja array2 on vastavalt esimene ja teine
andmeblokk.

Tulemusena väljastatakse eelnevalt
valitud lahtrisse korrelatsioonikordaja r väärtus, mis
antud juhul (tudengite pikkuste ja kaalude analüüsil) on 0,9065.
|
|
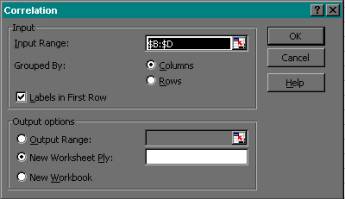
Protseduur Correlation
Mitme tunnuse korral on paarikaupa
korrelatsioonikordajate tabeli (korrelatsiooni-
maatriksi) arvutamiseks kasutatav protseduur Correlation
(Tools -> Data Analysis).
Avanevas sisestusaknas tuleb määrata:
Input Range - algandmete blokk (tunnused peavad paiknema
järjestikustes veergudes);
Grouped by - määratakse, kas tunnusvektorid on
orienteeritud veerge pidi
(Columns) või ridu pidi (Rows);
Labels in First Row - märgitakse nimede või tähiste
olemasolu korral tunnuste bloki esimeses reas;
Output options - määratakse tulemuste väljastamise
asukoht: samale töölehele
(Output Range), uuele töölehele (New Worksheet Ply) või
uude faili (New
Workbook).
Tulemuseks on Exceli töölehele
väljastatav kolmnurkse kujuga korrelatsioonikordajate maatriks:
| |
Pikkus |
Kaal |
Mat.hinne |
| Pikkus |
1 |
| Kaal |
0.90652 |
1 |
| Mat.hinne |
-0.16377 |
-0.223 |
1 |
|
|
Korrelatsioonikordajaga kirjeldatava
lineaarse seose statistiline olulisus
Korrelatsioonikordaja statistilise
olulisuse kontrollimine seisneb hüpoteeside
paari H0: r = 0;
H1: r ¹
0;
kontrollimises.
Kahjuks ei väljasta Excel korrelatsioonanalüüsi läbi viies
automaatselt taoliste hüpoteeside kontrollimiseks vajalikke
näitajaid (korrelatsioonikordaja või teststatistiku kriitilist
väärtust või olulisustõenäosust p). Lahendusena võib
kõne alla tulla vähemalt kolm varianti.
- Esiteks võib kasutada korrelatsioonikordajate
kriitiliste väärtuste tabelit, mis on leitav
enamuse statistikaõpikute lisades -- kui teie andmetel leitud
korrelatsioonikordaja r väärtus on suurem vastavast
kriitilisest väärtusest rkr (viimane sõltub
kordaja arvutamisel kasutatud väärtustepaaride arvust n
ja olulisusnivoost a),
võite lugeda tõestatuks hüpoteesi korrelatsioonikordaja nullist
erinevuse osas (seose olemasolu), vastasel juhul olete sunnitud
jääma nullhüpoteesi juurde.
-
Teine võimalus uuritava lineaarse seose statistilise olulisuse
kontrollimiseks on teostada kahe uuritava tunnusega tavaline lineaarne
regressioon protseduuri Regression abil. Lineaarse
regressiooniseose statistilist olulisust iseloomustav olulisuse tõenäosus
p kehtib ka lineaarse korrelatsioonikordaja jaoks (täpsemalt
regressioonanalüüsi teostamisest Exceliga vt järgmisest
peatükist).
- Kolmas võimalus on leida olulisuse
tõenäosuse p väärtus tuginedes ülaltoodud hüpoteeside
kontrollimisel arvutatavale teststatistikule
t = r Ö(n-2)
/ Ö(1-r2),
mis on nullhüpoteesi kehtides t-jaotusega parameetriga n-2.
Olulisustõenäosuse arvutamiseks on kasutatav Exceli
funktsioon TDIST(t;n-2;2), kus
esimesena argumendina tuleb ette anda eelnevalt toodud
teststatistiku t väärtus.
Kui p < 0,05, võime lugeda kahe tunnuse vahelise seose
statistiliselt oluliseks
|
ktanel@eau.ee
http://ph.eau.ee/~ktanel/kool_ja_too/
nov, 2003
|