Chart Wizard

  
Chart Wizard

Kahe tunnuse vahelisest sõltuvusest visuaalse ülevaate saamiseks on analüüsi esimese sammuna kasulik teha nende tunnuste vaheline hajuvusdiagramm (scatter plot).

Näiteks tudengite pikkuste ja kaalude vahelise seose iseloomustamiseks saame alljärgneva toodud graafiku.

Lihtsaim viis kahe tunnuse vahelise regressioonanalüüsi tegemiseks on:

• aktiveerida joonis;
• valida menüüst Chart käsk Add Trendline…;
• valida avanenud menüüst punktiparve kuju paremini jälgiv regressioonijoon (peale tavalise lineaarse regressiooni - Linear - on punktiparvele sobitatavad ka mitmed keerulisemad kõverad);
• valida samast Add Trendline…-aknast (sama aken avaneb ka peale hiire parempoolse nupu topeltklõpsu trendijoonel) lipik Options ja märkida seal ära käsud Display equation on chart ja Display R-squared value on chart.

Tulemuseks on joonis, kus lisaks punkti parvele on kujutatud ka regressiooni joon, regressioonivõrrand ja determinatsioonikordaja R².

Antud näite korral on meil tudengi kaal prognoositav tema pikkusest valemiga
Kaal = -107,5 + 0,9967*Pikkus,
kusjuures selline mudel võimaldab ära kirjeldada 82% tunnuse 'Kaal' hajuvusest.

NB! Joonise tegemisel paigutage vertikaalsele teljele (y-teljele) uuritav (prognoositav) tunnus ja horisontaalteljele (x-teljele) argumenttunnus.
  

  
Protseduur Regression

Täieliku lineaarse regressioonanalüüsi tegemiseks on MS Exceli keskkonnas protseduur Regression (Tools -> Data Analysis).
Erinevalt Chart Wizard'st või funktsioonidest võimaldab see teostada ka mitmest regressioonanalüüsi, argumenttunnuste blokid peavad siis vaid paiknema üksteise kõrval (et neid saaks ette anda ühe pideva andmeblokina)

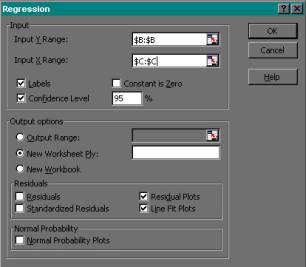
Protseduuri sisestusaknas tuleb määrata:

  Input Y Range - funktsioontunnuse andmete blokk;
  Input X Range - argumenttunnus(t)e andmete blokk;
  Labels - märgitakse nimede või tähiste olemasolu korral tunnuste bloki esimeses reas;
  Constant is Zero - märgitakse, kui tahetakse kontrollida tunnuste vahelist võrdelist sõltuvust (vabaliige a = 0);
  Confidence Level - usaldusnivoo parameetrite 1-a usalduspiiride arvutamiseks;
  Output options - määratakse tulemuste väljastamise asukoht: samale töölehele (Output Range), uuele töölehele (New Worksheet Ply) või uude faili (New Workbook).

Nende sisestuste põhjal moodustatakse kolm tabelit lineaarse regressioonanalüüsi parameetrite hinnangute, nende veahinnangute ja dispersioonanalüüsiga.

Soovi korral võib sisestusaknas täiendavalt tellida:

  Residuals - kõigi vaatluste prognoosijäägid;
  Standardizised Residuals - kõigi vaatluste standardiseeritud prognoosijäägid;
  Residuals Plot - prognoosijääkide graafik argumenttunnuse suhtes;
  Line Fit Plot - funktsioontunnuse ja prognooside graafik argumenttunnuse suhtes;
  Normal Probability Plot - funktsioontunnuse empiiriliste kvantiilide graafik (tõenäosuspaber).

Protseduuri Regression väljund

  
Protseduur Regression võimaldab väljastada ka kolm joonist:

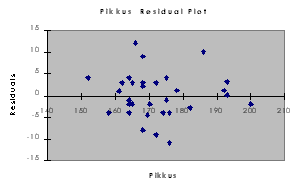
Neist esimene, valikuga Residuals Plot tellitav, iseloomustab prognoosijääkide paiknemist argumenttunnuse suhtes. Kui regressioonanalüüsi eeldused on täidetud, peavad punktid sellel graafikul paiknema juhuslikult, ühtlaselt hajutatud punktiparvena.

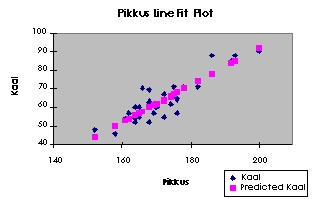
Teine, valikuga Line Fit Plot tellitav graafik, näitab funktsioontunnuse ja prognooside paiknemist argumenttunnuse suhtes. See graafik on analoogne Chart Wizard'i abil saaduduga, kus hajuvusdiagrammile lisati lineaarne regressioonijoon (ka sellel graafikul võib prognoosidele vastavad punktid omavahel ühendada, saades nii regressioonisirge). Selline pilt on põhiline kahe tunnuse vahelise seose illustreerimiseks kasutatav joonis.

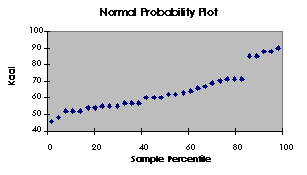
Kolmas, valikuga Normal Probability Plot tellitav graafik, on jällegi kasutatav regressioonanalüüsi eelduste täidetuse kontrollimiseks. Ideaalvariandis paiknevad selle graafiku punktid ühel diagonaalsel sirgel. Kui see nii ei ole, ei jaotu uuritav tunnus vastavalt normaaljaotusele.