Keskväärtuste võrdlemine võrdse dispersiooniga üldkogumite korral

Kui funktsiooni FTEST poolt väljastatud olulisuse tõenäosus p >= 0,05, oleme sunnitud jääma nullhüpoteesi juurde, st. et varieeruvus kahes võrreldavas üldkogumis on ühesugune. 
Sellisel juhul saame nende üldkogumite keskväärtusi võrrelda protseduuri t-Test: Two Sample Assuming Equal Variances abil.

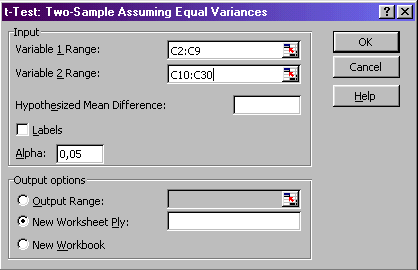
Protseduuri tellimisaknas tuleb täita järgmised väljad:
   Variable 1 Range - suurema aritmeetilise keskmisega valimi andmete blokk;
   Variable 2 Range - väiksema aritmeetilise keskmisega valimi andmete blokk;
   Hypothesized Mean Difference - oletatav keskväärtuste erinevus (vaikimisi null);
   Labels - märgitakse nime või tähise olemasolul andmebloki esimeses reas;
   Alpha - olulisuse nivoo (vaikimisi 0,05);
   Output options - määratakse tulemuste väljastamise asukoht: samale töölehele (Output Range), uuele töölehele (New Worksheet Ply) või uude faili (New Workbook).

Rakendades seda protseduuri F-testi peatüki lõpus vaadeldud mannaputru armastavate ja mittearmastavate tudengite kaalude erinevuse selgitamiseks, täidame väljad tellimisaknas

ja saame tulemuseks järgmise tabeli:

Saadud tulemuste põhjal veendume, et tudengite kehakaal ei sõltu nende mannapudrulembusest, sest vastav olulisuse tõenäosus p = 0,796 > 0,05. Samuti ei saa me väita, et mannaputru süüa armastavate tudengite kehakaal oleks oluliselt suurem (p = 0,381).
  

  
Keskväärtuste võrdlemine mittevõrdse dispersiooniga üldkogumite korral

Kui funktsiooni FTEST poolt väljastatud olulisuse tõenäosus p < 0,05, võime lugeda tõestatud sisuka hüpoteesi üldkogumite erinevast varieeruvusest. 
Sellisel juhul saame nende üldkogumite keskväärtusi võrrelda protseduuri 
 t-Test: Two Sample Assuming Unequal Variances abil.

Protseduuri sisend ja väljund on analoogsed eelneva (keskmiste võrdlemisel t-testiga võrdsete dispersioonide korral kasutatud) protseduuriga. Vaid väljundtabelis on üks rida vähem - et dispersioonid on erinevad, ei kasutata arvutamisel enam ühendatud valimi dispersiooni (Pooled Variance).
   

   
Kahe üldkogumi keskväärtuste võrdlemine sõltuvate vaatluste korral

Sõltuvate valimite (mõõdetud on ühtesid ja samu objekte, enne ja pärast teatavat "katset") keskväärtuste võrdlemiseks on kasutatav protseduur
 t-Test: Paired Two Sample for Means.

Protseduuri sisend ja väljund on jällegi analoogsed eelnevate (keskmiste võrdlemisel t-testiga võrdsete või mittevõrdsete dispersioonide korral kasutatud) protseduuridega. Vaid väljundtabelis on nimetuse Pearson Correlation taga ära toodud võrreldavate tunnuste vaheline Pearsoni seosekordaja.
   

  
Kahe üldkogumi keskväärtuste võrdlemine - t-test

Funktsioon TTEST(Array1,Array2,Tails,Type)

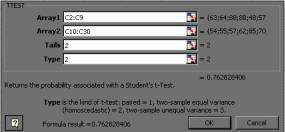
Kahe üldkogumi keskväärtuste võrdlemiseks nii sõltuvate kui ka sõltumatute vaatluste ning nii võrdsete kui ka mittevõrdsete dispersioonide korral on kasutatav ka funktsioon TTEST(Array1,Array2,Tails,Type).

Funktsiooni argumentidena tuleb sisestada:

   Array1 - esimese valimi andmete blokk;
   Array2 - teise valimi andmete blokk (mõlemad ilma tunnuse nimeta);
   Tails - hüpoteesi tüüp (1 - ühepoolne, 2 - kahepoolne hüpotees);
   Type - määratakse, millist tüüpi eeldusega on tegu: 1 - sõltuvad valimid, 
             2 - võrdsed dispersioonid, 3 - erinevad dispersioonid.

Kontrollides siin kahepoolset hüpoteesi (Tails = 2) tudengite kehakaalude erinevuse kohta sõltuvalt nende mannapudru lembusest ja arvestades eelnevat F-testi tulemust (dispersioonid on võrdsed - Type = 2), saame tulemuseks olulisuse tõenäosuse p = 0,76 (keskmised ei ole erinevad), mis langeb kokku eelnevalt protseduuriga t-Test: Two Sample Assuming Equal Variances saadud tulemustega.